(github个人网址)[]
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | 20 | 30 |
| · Estimate | · 估计这个任务需要多少时间 | 10 | 10 |
| Development | 开发 | 400 | 700 |
| · Analysis | · 需求分析 (包括学习新技术) | 60 | 90 |
| · Design Spec | · 生成设计文档 | 30 | 40 |
| · Design Review | · 设计复审 (和同事审核设计文档) | 60 | 120 |
| · Coding Standard | · 代码规范 (为目前的开发制定合适的规范) | 30 | 30 |
| · Design | · 具体设计 | 30 | 50 |
| · Coding | · 具体编码 | 90 | 300 |
| · Code Review | · 代码复审 | 40 | 70 |
| · Test | · 测试(自我测试,修改代码,提交修改) | 60 | 100 |
| Reporting | 报告 | 50 | 80 |
| · Test Report | · 测试报告 | 70 | 110 |
| · Size Measurement | · 计算工作量 | 5 | 10 |
| · Postmortem & Process Improvement Plan · | 事后总结, 并提出过程改进计划 | 15 | 20 |
| 合计 | 670 | 1160 |
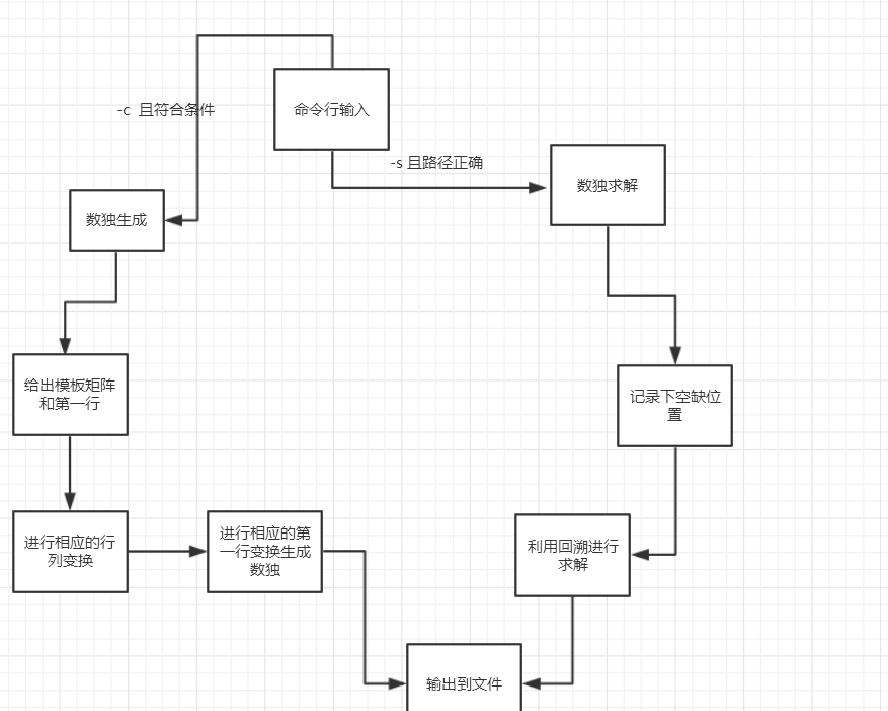
解题思路描述。即刚开始拿到题目后,如何思考,如何找资料的过程。
数独生成
在初始阶段的想法是,将整个9*9数独分为九个3*3 的小的九宫格,然后按照每个小九宫格(从左到右,从上到下)的顺序填入。 每次只填入一个数字(如首先将1填入到各个小的九宫格中),在所有1填完的基础上再填2,以此类推等等。 这种思路的优势有两个:第一,这种思路比较简单易懂,在不考虑效率的情况下,实现起来比较快,而且出错的可能性也比较小;其次,我们通过回溯的方式将最终生成的一个数独进行回溯,避免了一些相同部分数独生成的重复工作,而且因为按照一定顺序遍历,可以有效避免重复数独的出现,同时,因为我们每次填入都是对不同小九宫格的相同数字的位置,可以在检查是否能够填入的时候不检查九宫格内部的情况,而且最后一个填入的数字完全不用在意位置,直接填入即可,在一定程度上减少了运算量。 下面具体就可能出现的问题进行分析: (1)因为题目要求了开头数字,我的是(6+9)%9+1=7,那么我们在填入的时候可以不按照原先的1,2……9的顺序填入,而是按照7,8,9,1……6的顺序填入 ,在算法实现上没有任何区别。 (2)如何进行回溯:我们每次在要填入的小九宫格中按照一定顺序判断是否能够填入数字,如果该九宫格中没有一个合适的位置进行填入,那么我们就将上一个填入的数字重新归零,再选择一个其他的位置进行填入,直至找到一个能够完全填满的方式,然后再将最后一个填入的数字归零,依次往前,直到找到一种与原先所填位置不同的数字,再依次向下填,直至再次找到一个完成的数独,重复以上操作直至生成数独数目达到要求。 这种方法的缺陷是比较直接粗暴所导致运行效率不够高,速度比较慢。 然后我就有了第二种思路,我们可以知道,只交换数独内部(指3*3的小数独)所得出的结果依然是一个数独,在这种思路的指导下,我们可以通过一个数独的第一行和一个标准的完整数独生成一个新的数独,再通过交换行和列生成一些新的数独,因为第一个数字是固定的,所以第一行和第一列不能交换,那么交换方式共有2*6*6*2*6*6=5184,远远不够1000000种,那么我们可以将第一行除了第一个数字的其余8个数字进行全排列,那么所得出的结果远远大于1000000种(有些同学可能会考虑到有可能发生重复的情况,但是通过数学方法可以证明,这种情况下生成的数度不会发生重复),这种方式更为简单直接,而且在代码书写方面也比较直接,同时运行效率优于前面所说的方法。 注意事项: 我们可以每次通过交换的第一行将代码进行变换,比如模板的(0,0)为1,而我们的要求(0,0)是7,那么我们可以将所有模板中是1的位置替换成7,以此类推。 我们可以通过字典序的方式依次生成第一行后面8位数字的顺序,再进行变换。
数独求解
数独求解我用的是比较原始的递归回溯算法,这种算法比较直接,所以导致计算量比较大,因而速度上有一定的劣势。 具体思路: 我们首先将数独中空缺的部分记录下来,然后依次判断1-9在各个位置上是否能填入,如果能的话则将其填入,进行下一个空缺位置的填入,如果某一个位置不能继续填入,那么回溯到上一层,将上一层所填入的数字清0,重复上述过程,直到所有位置都填入成功,生成数独的一个解。
设计实现过程。设计包括代码如何组织,比如会有几个类,几个函数,他们之间关系如何,关键函数是否需要画出流程图?单元测试是怎么设计的?
记录在改进程序性能上所花费的时间,描述你改进的思路,并展示一张性能分析图(由VS 2017的性能分析工具自动生成),并展示你程序中消耗最大的函数。
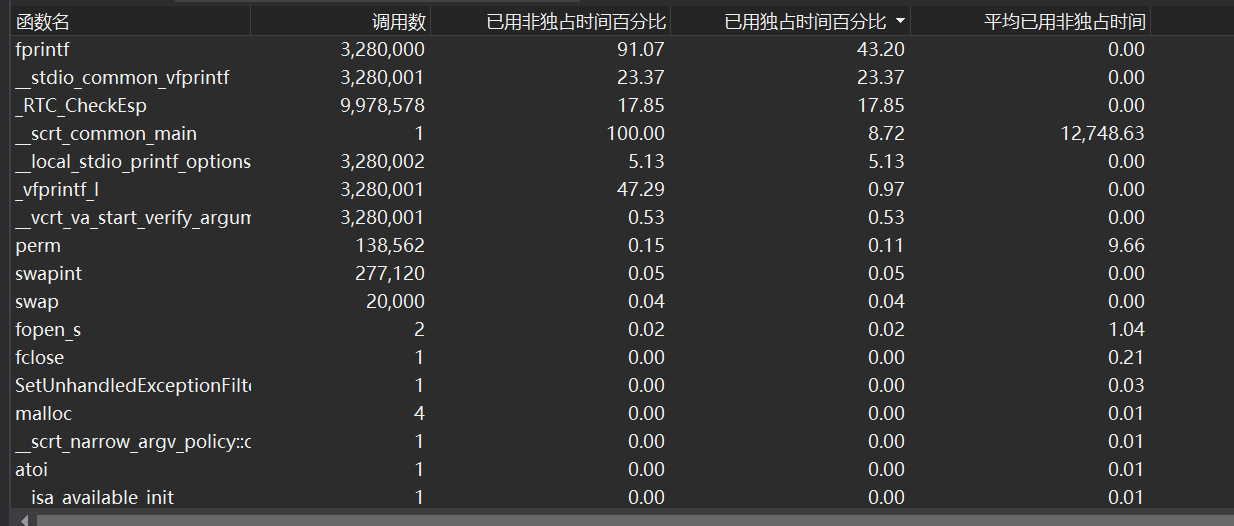
消耗比较大的主要是fprintf这个输出函数,因为每次只输出一个数字,导致整体输出的消耗很大,可以考虑用文件流的方式进行输出。
读入函数的消耗也很大,看来程序运行速度的减慢主要是输入输出导致的,可以在改进的时候考虑用文件流的方式。代码说明。展示出项目关键代码,并解释思路与注释说明。
部分代码
void solve(int solvednum,int sumnum, int sudoku[9][9], int emptyline[], int emptyqueue[]){ if (solvednum>81) { printf("sdsda"); } int k = 0; haveend = 0;//一个全局变量,表示是否已经完成求解 int i = emptyline[solvednum]; int j = emptyqueue[solvednum]; //bool a = false; //a = canin(6, 5, 6, sudoku); if (solvednum >= sumnum) { haveend= 1;//当solvednum >= sumnum表示恰好完成了求解 return; } else { for (k = 1; k < 10; k++) { if ((canin(i, j, k, sudoku)) == true) { sudoku[i][j] = k; solve(solvednum + 1, sumnum, sudoku, emptyline, emptyqueue);//更深层的递归 if (haveend==1) { return; } else { sudoku[i][j] = 0; } } } }} 然后依次判断1-9在各个位置上是否能填入,如果能的话则将其填入,进行下一个空缺位置的填入,如果某一个位置不能继续填入,那么回溯到上一层,将上一层所填入的数字清0,重复上述过程,直到所有位置都填入成功,生成数独的一个解
bool canin(int i,int j, int numinto,int sudoku[9][9]){ int n = i *9+ j; int k = 0; int p = 0; int q = 0; //先判断该行是否符合要求 for (k = 0; k < 9; k++) { if (sudoku[i][k] == numinto) { return false; } } //判断列是否符合要求 for (k=0;k<9;k++) { if (sudoku[k][j] == numinto) { return false; } } //判断是否符合小九宫格 /* x为n所在的小九宫格左顶点竖坐标 */ int x = n / 9 / 3 * 3; /* y为n所在的小九宫格左顶点横坐标 */ int y = n % 9 / 3 * 3; for (p= x; p < x + 3; p++) { for (q = y; q < y + 3; q++) { if (sudoku[p][q] == numinto) { return false; } } } return true; } 每次通过交换的第一行将代码进行变换,比如模板的(0,0)为1,而我们的要求(0,0)是7,那么我们可以将所有模板中是1的位置替换成7,以此类推。
int* transform(int firstline[],int modelsudoku[] ){ int *temp = (int*)malloc(sizeof(int)*81) ; int i = 0; int j = 0; int k = 0; for (k = 0; k < 9; k++) { temp[k] = firstline[k]; } for (i = 9; i < 81; i++) { for (j = 0; j < 9; j++) { if (modelsudoku[i] == modelsudoku[j]) { temp[i] = temp[j]; } } } int m = 0; return temp;}